在刷LeetCode时遇到了很多题目关于双指针,个人便萌生了对于双指针的使用进行一下总结的想法,昨天又碰巧看见LeetCode上一篇关于双指针常用技巧的总结文章(文末附有文章链接),大佬的思路清晰,读来令人醍醐灌顶,因此我想按照大佬的思路并结合自己所刷题目对于双指针进行如下总结:
总体来说,双指针分为两类:
(1)快慢指针:快慢指针常用与解决链表的问题,如判断链表中是否有环,寻找链表环起点等等;
(2)左右指针:左右指针则多处理字符串和数组的问题。
但在刷题过程中,这两种指针的使用与其对应的对象并不绝对。在实际的使用中,快慢指针在某些特定场景下往往有出奇制胜的效果,我们应该结合所面对的问题,灵活地使用双指针。
一、快慢指针
快慢指针顾名思义是使用两个指针fast和slow,fast指针在前、slow指针在后协同解决一些场景的问题。
1.判断链表是否含有环路
判断是否存在环路的思路很简单,fast指针前进的速度要比slow指针要快,如果fast指针走到了链表尾部被赋值为null,则没有环路;反之,fast指针如果与slow指针相遇了,则证明链表中存在环路。代码如下所示:
1 public boolean hasCycle(Listnode head) { 2 ListNode fast,slow; 3 fast = slow = head; 4 //判断是否有环 5 while(fast != null && fast.next != null){ 6 //快指针一次走两步 7 fast = fast.next.next; 8 //慢指针一次走一步 9 slow = slow.next; 10 if(slow == fast){ 11 return true; 12 } 13 } 14 return false; 15 }
2.已知有环,判断环路的起始节点
这个问题简单来说思路是这样的:快指针每次走两步,慢指针每次走一步,当两者相遇时,将其中任意一个指针重新指向头结点,让两个指针步调一致前进(每次都走一步),当它们再次相遇时,所指向的结点就是环路的起始节点。代码如下所示:
1 public ListNode detectCycle(ListNode head) {
2 ListNode fast,slow;
3 fast = slow = head;
4 //先判断是否有环
5 while( fast != null && fast.next != null){
6 fast = fast.next.next;
7 slow = slow.next;
8 if(slow == fast){
9 break;
10 }
11 }
12 //重置某一个指针的位置,让两者重新相遇
13 slow = head;
14 while(slow != fast){
15 slow = slow.next;
16 fast = fast.next;
17 }
18 return slow;
19 }那么为什么当两个指针重新相遇时,其结点就是环路的入口呢?这个问题是可以用严谨的公式推导的,但我在这里就参照 labuladong大佬的示意图,简单说明下思路:
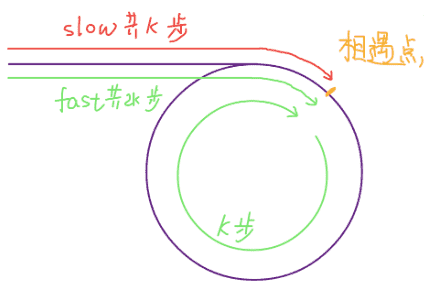
图一所示,当第一次相遇时,假设slow指针前进了k步,则fast指针前进了2k步,那么环路的长度也应该是k步;
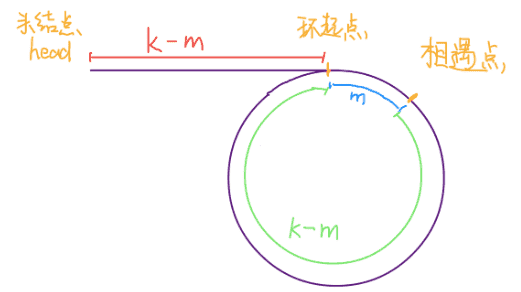
图二所示,此时假设相遇的点距离环路入口相距m步,因为slow前进了k步到达相遇点,则头结点距离环起点的位置就是k-m步;而因为环的长度也为k步,那么从环内出发,到达环路入口的距离也为k-m步;
因此当第一次相遇之后,将任意一个结点重置为头结点,让其以相同的步调前进再次相遇时,所指向的结点一定是环路的入口位置。
问题的变种:
LeetCode编号287题目是该问题的变种,可以将其转换为寻找链表环路入口的问题,题目描述如下所示:

单看题目描述,此题并不足以被认为是难度中等的题目,但题目的附加说明要求限制了普通方法的使用,例如先排序再相邻比对等;而采用双指针方法便能在符合要求的情况下解决这个问题,参照另一位大佬kirsche的题解,首先我们可以将这个题目转换为寻找循环链表的环路入口的问题,符合题目要求的数组nums其实是可以被视为一个存在环路的链表的,举例说明该问题:
整数的数组 nums中的数字范围是[1,n]。考虑一下两种情况: 如果数组中没有重复的数,以数组[1,3,4,2]为例,我们将数组下标n和数nums[n]建立一个映射关系f(n),
其映射关系n->f(n)为:
0->1
1->3
2->4
3->2
我们从下标为0出发,根据f(n)计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。这样可以产生一个类似链表一样的序列。
0->1->3->2->4->null
如果数组中有重复的数,以数组[1,3,4,2,2]为例,我们将数组下标n和数nums[n]建立一个映射关系f(n),
其映射关系n->f(n)为:
0->1
1->3
2->4
3->2
4->2
同样的,我们从下标为0出发,根据f(n)计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推产生一个类似链表一样的序列。
0->1->3->2->4->2->4->2->……
如果理解了以上如何将符合题意的数组nums视为一个存在环路的链表,那么现在这个问题就与寻找存在环路链表的环路入口问题等价了,可以采用快慢指针的方法解决该问题,需要特别注意的是快慢指针赋值的方式:
慢指针每次走一步:slow = nums[slow]
快指针每次走两步:fast = nums[ nums[fast] ]
具体解题代码如下所示:
1 public int findDuplicate(int[] nums) {
2
3 int fast = nums[nums[0]];
4 int slow = nums[0];
5
6 //第一次相遇
7 while(fast != slow){
8 fast = nums[nums[fast]];
9 slow = nums[slow];
10 }
11
12 //从头结点开始,走到再次相遇
13 slow = 0;
14 while(fast!=slow){
15 slow = nums[slow];
16 fast = nums[fast];
17 }
18
19 return slow;
20 }3.寻找链表的中点
该问题的思路很简单,同样是快指针每次走两步,慢指针每次走一步,当快指针到达链表尾部时,如果链表长度是奇数,则慢指针刚好处于链表中点;如果链表长度是偶数,则慢指针所在的位置是中间偏右。这样就很方便的定位到了链表的中点,定位链表的中点的一个重要应用是对链表进行归并排序。
4.寻找链表倒数第k个元素
这个问题的思路其实与定位链表中点类似,只不过快慢指针之间的差距不再是固定的步伐了,而是固定的距离;我们结合一道具体的题目来说明这个问题:
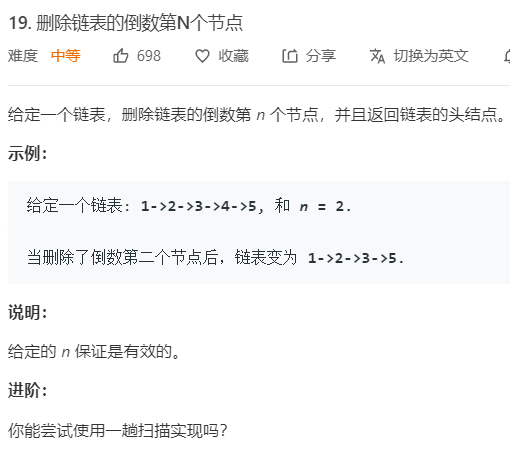
先用一个哑指针作为辅助,让快慢指针从哑指针开始,先让快指针前进n步,再让两个指针同速前进,直到快指针到达了链表的最后一个结点,则慢指针也到达了需要删除的指针的前一个指针,删除结点,代码如下所示:
1 public ListNode removeNthFromEnd(ListNode head, int n) {
2 //辅助哑结点
3 ListNode dummy = new ListNode(0);
4 dummy.next = head;
5 ListNode fast,slow;
6 fast = slow = dummy;
7
8 //让快指针先走n步
9 for(int i = 0;i<n;i++){
10 fast = fast.next;
11 }
12
13 //快慢指针同速前进,直到快指针到达链表尾部
14 while(fast.next!=null){
15 fast = fast.next;
16 slow = slow.next;
17 }
18 slow.next = slow.next.next;
19 return dummy.next;
20 }二、左右指针
左右两个指针一般是数组的两个索引,最适用于有序的数组。
1.二分查找
二分查找是最典型的左右指针的适用场景了,就不再赘述了,直接贴代码,算是复习回忆一下:
1 int binarySearch(int[] nums, int target) {
2 int left = 0;
3 int right = nums.length - 1;
4 while(left <= right) {
5 int mid = (right + left) / 2;
6 if(nums[mid] == target)
7 return mid;
8 else if (nums[mid] < target)
9 left = mid + 1;
10 else if (nums[mid] > target)
11 right = mid - 1;
12 }
13 return -1;
14 }2.三数之和
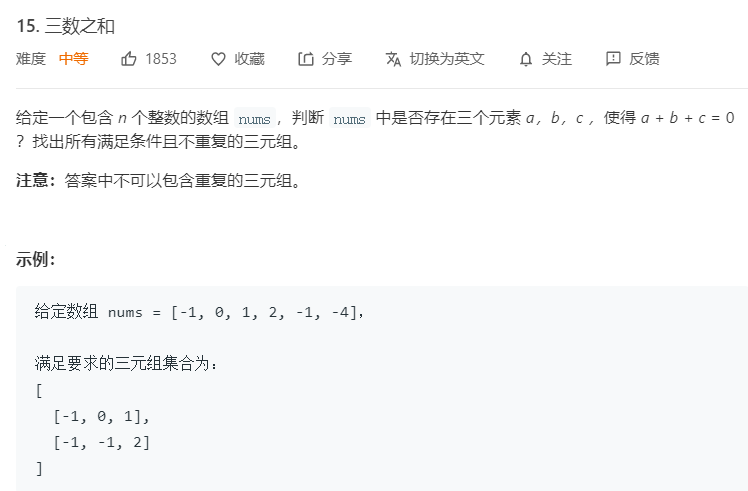
这也是很经典的一道算法题了,大致思路是:先对于数组进行排序,然后固定3个指针中最小数字的指针k,然后通过左右指针i和j在数组索引两端,通过交替向中间移动遍历数组,记录满足条件的三元组,具体代码如下所示(实现的细节参照代码注释):
1 public List<List> threeSum(int[] nums) {
2 //先对数组进行排序
3 Arrays.sort(nums);
4 List<List> tem = new ArrayList<>();
5
6 for(int k=0;k0) break;
9 //跳过重复的数
10 if(k > 0 && nums[k] == nums[k-1]) continue;
11 //设置双指针
12 int i = k+1;
13 int j = nums.length - 1;
14 //左右指针对数组进行遍历
15 while(i<j){
16 int sum = nums[k] + nums[i] + nums[j];
17 //如果三数之和小于0,则移动左指针,并且跳过重复的数
18 if(sum < 0){
19 while(i < j && nums[i] == nums[++i]);
20 //如果三数之和大于0,则移动右指针,并且跳过重复的数
21 }else if(sum >0){
22 while(i < j && nums[j] == nums[--j]);
23 }
24 if(sum == 0){
25 tem.add(new ArrayList(Arrays.asList(nums[k], nums[i], nums[j])));
26 while(i < j && nums[i] == nums[++i]);
27 while(i < j && nums[j] == nums[--j]);
28 }
29 }
30 }
31 return tem;
32 }3.滑动窗口
滑动窗口算是比较高阶的双指针用法,多用于处理字符串字串的匹配问题,为了更好的理解问题我们还是结合题目来说明:
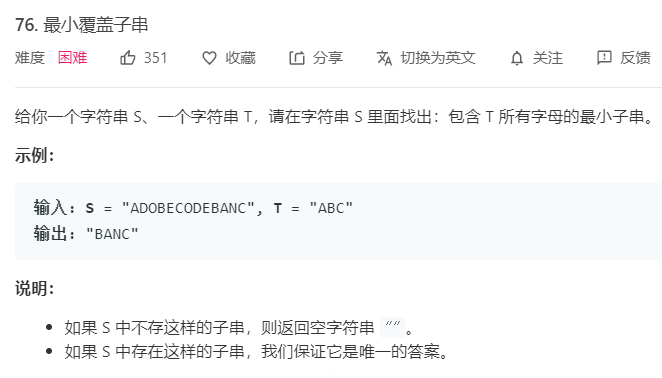
滑动窗口的思路是这样的:
1.初始化left=right=0,两者都指向字符串S,将闭区间[left,right]视为一个窗口。
2.先不断增加窗口的右端,扩大窗口right++,直到窗口包含了所有的需要的字符。
3.此时停止增加right,开始增加窗口左端,缩小窗口left++,直到窗口不符合包含字符的要求,停止,并更新最小窗口的大小。
4.重复第2、3步,直到right到达字符串S的尽头。
算法伪代码如下所示:
1 String s,t; 2 int left = 0, right = 0; 3 String res = s; 4 5 while (right < s.length()) { 6 window.add(s[right]); 7 right++; 8 //如果满足包含字符条件 9 while (valid) { 10 //更新最小子串 11 res = minLen(res,window); 12 window.remove(s[left]); 13 left++; 14 } 15 } 16 17 return res;
如果你完全理解了以上的思路,你就已经掌握了滑动窗口的核心思想;但可能还有一个问题没有解决,如何判断 window 即子串 s[left...right] 是否符合要求,是否包含 t 的所有字符呢?在这里我们可以使用两个长度为128数组来作为计数器,长度为128是考虑到字符的ASCII码,needs数组计数目标子串字符出现的次数;window数组计数窗口中字符出现的次数。labuladong大佬给出的方案是使用两个哈希表作为计数器,哈希表当然是适用于所有情况的,数组可以根据具体情况使用,在性能上可能略优于哈希表。(代码中需要注意match变量统计的是有多少种字符匹配成功,而不是多少次匹配成功)
本题的全部代码如下所示:
1 public String minWindow(String s, String t) {
2
3 //记录最短字串的开始位置和长度
4 int start = 0;
5 int minLen = Integer.MAX_VALUE;
6 int left = 0;
7 int right = 0;
8
9 //记录window中已经有多少种字符满足要求了
10 int match = 0;
11
12 //字符的ASCII码
13 int[] needs = new int[128];
14 int[] window = new int[128];
15
16 //初始化needs数组
17 for(char ch:t.toCharArray()){
18 needs[ch]++;
19 }
20
21 //计算t中包含了多少种不同的字符
22 int kinds = 0;
23 for(int i=0;i0){
25 kinds++;
26 }
27 }
28
29 while(right < s.length()){
30 char c1 = s.charAt(right);
31 window[c1]++;
32 //判断并更新match
33 if(needs[c1]>0 && window[c1]==needs[c1]){
34 match++;
35 }
36 right++;
37
38 //如果窗口向右扩展到所有字符都满足了,开始右移左边界
39 while(match == kinds){
40 //更新最小字串的位置和长度
41 if(right-left0 && window[c2]<needs[c2]){
48 match--;
49 }
50 left++;
51 }
52 }
53 return minLen == Integer.MAX_VALUE? "":s.substring(start,start+minLen);
54 }三、双指针的灵活使用
1.修改数组
不使用额外空间的情况下,根据场景条件对于数组进行过滤并完成修改。这样讲有点抽象,我们结合具体题目来理解:
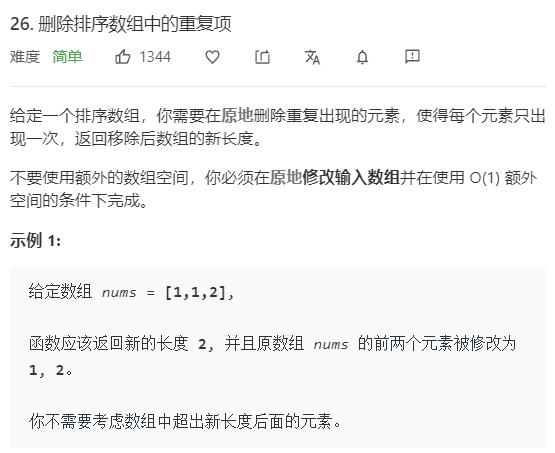
使用双指针删除重复的元素,初始化指针i=0;指针j=1;
1.如果nums[j] = nums[i];则j++;
2.如果nums[j]!=nums[i];则有nums[i+1]=nums[j]并且j++;i++;
这道题的思路我是这样理解的:将j指针视为过滤指针,而i指针则是执行拷贝修改的指针,如果满足删除条件,j++将其过滤掉;如果不满足删除条件,则需要i指针执行拷贝,将其保留下来。这样就完成了数组的原地修改拷贝,并返回数组的新长度i+1。代码如下所示:
1 public int removeDuplicates(int[] nums) {
2 int i = 0;
3 int j = 1;
4 while(j < nums.length){
5 if(nums[i] == nums[j]){
6 j++;
7 }else{
8 nums[i+1] = nums[j];
9 j++;
10 i++;
11 }
12 }
13 return i+1;
14 }