泰勒展开式「建议收藏」

大家好，又见面了，我是你们的朋友全栈君。

数学中，泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。

泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。

若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶导数，则对闭区间[a,b]上任意一点x，成立下式：

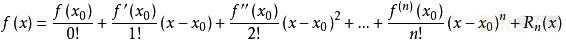
其中，f(n)(x)表示f(x)的n阶导数，等号后的多项式称为函数f(x)在x0处的泰勒展开式，剩余的Rn(x)是泰勒公式的余项，是(x-x0)n的高阶无穷小。

麦克劳林展开

函数的麦克劳林展开指上面泰勒公式中x0取0的情况，即是泰勒公式的特殊形式，若f(x)在x=0处n阶连续可导，则下式成立：

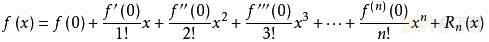
其中f(n)(x)表示f(x)的n阶导数。

实际应用中，泰勒公式需要截断，只取有限项，一个函数的有限项的泰勒级数叫做泰勒展开式。泰勒公式的余项可以用于估算这种近似的误差。

泰勒展开式的重要性体现在以下三个方面：

　　幂级数的求导和积分可以逐项进行，因此求和函数相对比较容易。

　　一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数，并使得复分析这种手法可行。

　　泰勒级数可以用来近似计算函数的值。

实例

1、展开三角函数y=sinx和y=cosx。

解：根据导数表得：

显然y=sinx在x=0处具有任意阶导数，并且

。

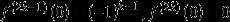
根据麦克劳林公式：

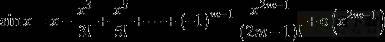
类似地，可以展开y=cosx。

2、计算近似值

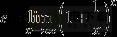
解：对指数函数

运用麦克劳林展开式并舍弃余项：

当x=1时：

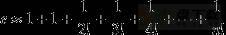
取n=10，即可算出近似值e≈2.7182818。

关于泰勒公式的感性理解 转自https://www.zhihu.com/question/50656047/answer/122146471

想象一个函数，你只能观测其中很小一段的图像，现在需要从这一小段预测其他点的函数值

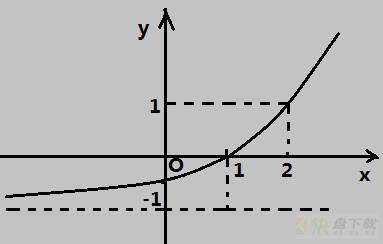
随便找了一张图，假设泰勒原点在x=0，即你只能观测x=0附近很小一段的函数图像

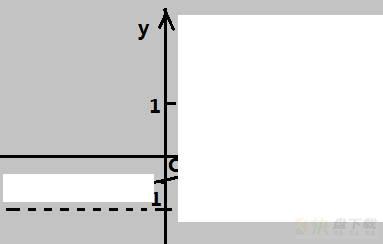
这时你可能会想，切线在这段符合得挺好，就用它估计吧，这条线的斜率就是f'(0)

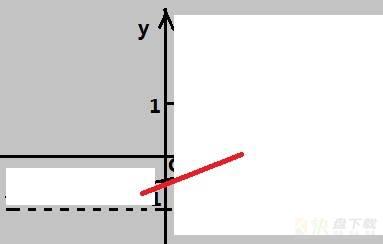
结果和实际相去甚远

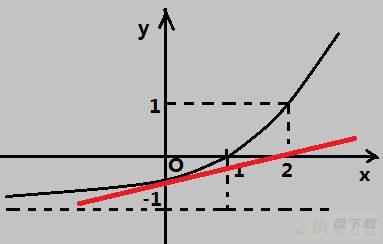
你可能会很奇怪，为什么看起来这么接近，结果还差这么大，就使劲盯着这段函数看啊看

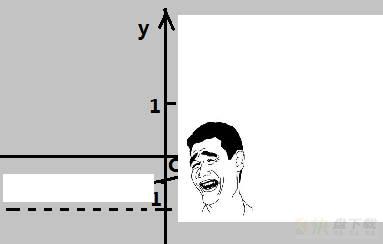
盯了半天，经过了n次放大，你终于发现曲线的左右比切线都要高一些，像是一条抛物线。于是你在切线的基础上加了一个抛物线因子，对应的二次斜率就是f”(0)/2

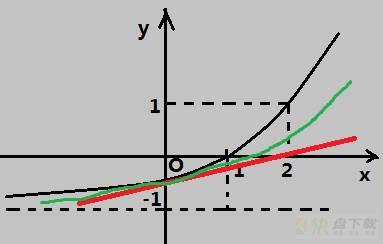
虽然还是很不准，还是比一开始的预测准了不少，于是你信心大增，很快发现了新的不同，利用三次曲线去预测

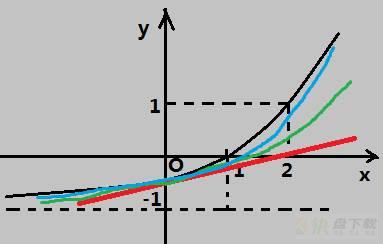
然后你会发现越来越准，直到预测了n次，你看得累了，预测结果和真实函数也差不多了，就把可能的最大偏差用一个余项表示，当然离原点越远就越不准，这个余项也和x有关。泰勒公式可以说是用函数在某一点的导数逐次逼近函数的过程。

发布者：全栈程序员栈长，转载请注明出处：https://javaforall.cn/167774.html原文链接：https://javaforall.cn