动态规划详解

在上例的多阶段决策问题中,各个阶段采取的决策;一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移;一个决策序列就是在变化的状态中产生出来的,故有“动态;的含义;称这种解决多阶段决策最优化问题的方法为动态规划方法。
与穷举法相比;动态规划的方法有两个明显的优点;

;1;大大减少了计算量。;2;丰富了计算结果

应用动态规划要注意阶段的划分是关键;必须依据题意分析;寻求合理的划分阶段(子问题)方法。而每个子问题是一个比原问题简单得多的优化问题。
动态规划适合解决什么样的问题?准确地说,动态规划不是万能的,它只适于解决一定条件的最优策略问题。

上面所说的“满足一定条件”主要指下面两点:(1)状态必须满足最优化原理;(⑵状态必须满足无后效性。
动态规划的最优化原理是无论过去的状态和决策如何;对前面的决策所形成的当前状态而言;余下的诸决策必须构成最优策略。
动态规划的无后效性

动态规划转移方程式也就是递推式。

例题1;

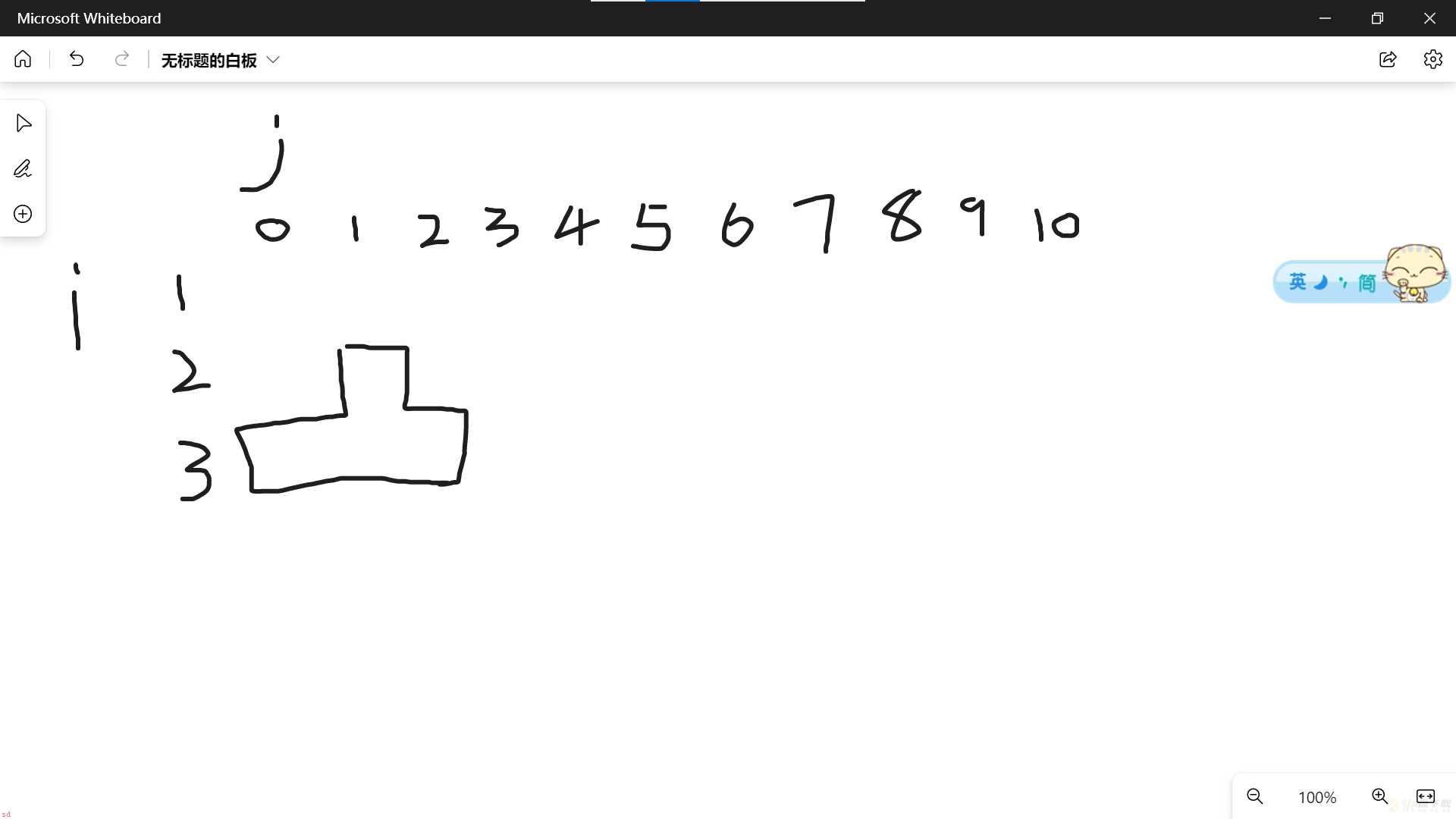
都说天上不会掉馅饼;但有一天 Gameboy 正走在回家的小径上;忽然天上掉下大把大把的馅饼。说来 Gameboy 的人品实在是太好了;这馅饼别处都不掉;就掉落在他身旁的 10m 范围内。馅饼如果掉在地上;当然就不能吃了;所以 Gameboy 马上卸下身上的背包去接。但由于小径两侧都不能站人;所以他只能在小径上接。由于 Gameboy 平时老待在房间里玩游戏;虽然在游戏中是个身手敏捷的高手;但在现实中运动神经特别迟钝;每秒只有在移动不超过 1m 的范围内接住坠落的馅饼。现在给这条小径标上坐标;如图 1 所示。

为了简化问题;假设在接下来的一段时间里;馅饼都掉落在 0;10 这 11 个位置。开始时 Gameboy 站在位置 5;因此在第 1 秒;他只能接到 4、5、6 这 3 个位置中 1 个位置上的馅饼。 问 Gameboy 最多可能接到多少个馅饼;假设他的背包可以容纳无穷多个馅饼;?

测试说明

Time limit 1000 ms Mem limit 32768 kB

平台会对你编写的代码进行测试;

测试输入;

6

5 1

4 1

6 1

7 2

7 2

8 3

0

预期输出;

4

试题来源

HDU 1176

据题意;当我们第T秒站在x点的时候;我们便可以在T;1秒的时候接到x-1;X,x;1这三个点其中的一个点的馅饼。
假设我们第T秒站在了x点;那么直到结束时最多能接到多少个馅饼呢?将其记为DP(T,x)。
而将在T秒站在x点正接到的馅饼数记为exactly(T,x)。

那么下一秒;即T;1秒就有可能站在x、x-1、x;1这三个点之中的一个点;有方程:

 DP[T,x]= exactly[T,x]; MAX( DP(T;1,x);DP[T;1,x-1],DP[T;1,x;1])

由这个方程可知;如果想要求第一秒的值;需要知道第二秒的;想要求第二秒的;需要知道第三秒的。所以如果求最后一秒的;只需要求exactly的值即可;然后依次往前推;就可以求得所有的。

由于DP的值是一个累积量;所以从前往后求和从后往前求的结果是一样的。例如1;2;3;4;计算的顺序不影响最后的结果。

其中DP叫做状态转移方程;exactly叫做初值表达式。

在写代码的时候把他们看成二维数组。

代码如下;

#include<iostream>
#include<string.h>
using namespace std;
int exactly[100110][12];//保存第 i秒 j 位置落下的馅饼
int dp[100110][12];//保存第 i秒 j 位置 最多还能接到的馅饼
main()
{
	int n;
	int i,j;
	int x,t;
	int max1=0,max2;
	while(scanf(%d;,&n),n!=0)
	{
		memset(exactly,0,sizeof(exactly));//将数组重置 
		memset(dp,0,sizeof(dp));
		for(i=1; i<=n; i;;)//先将exactly表格填好
		{
			scanf(%d%d;,&x,&t);
			exactly[t][x];;; //正接到的馅饼数  横着看时间;竖着看位置
			if(t>max1)
			{
				max1=t;
			}
		}
		for(i=0; i<=10; i;;)//将最后一秒的dp值填好
		{
			dp[max1][i]=exactly[max1][i]; //最后1秒的dp值直接来自于exactly
		}
		for(i=max1-1; i>=0; i--)//
		{
			for(j=0; j<11; j;;)//一共11个位置 
			{
				//按照dp状态转移方程来求解;将dp填充完整 
				max2=0;
				if(j-1>=0)//形成一个梯形;表示左边的 ;当j为0的时候;就没有左边的 
				{
					max2=dp[i;1][j-1];
				}
				if(dp[i;1][j]>max2)//正下方的 
				{
					max2=dp[i;1][j];
				}
				if(dp[i;1][j;1]>max2&&(j;1<=10))//右边的 ;当j为10时;就没有右边的 
				{
					max2=dp[i;1][j;1];
				}
				dp[i][j]=exactly[i][j];max2;
			}
		}
		printf(%d
;,dp[0][5]);//输出第0秒所在的起始位置 
	}
	return 0;
}